安徽,[11月11日]数学《高考数学文科小题狂做基础篇全国卷第4版》P56/Q16疑问是为什么前(n-1)个数集所有元素个数之和为n(n-1)/2
题目:已知元素为正整数的数集序列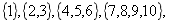 …,从第二个数集开始,每一个数集比前一个数集多一个元素,且每一个数集中最小的元素比前一个数集中的最大的元素大1,则第n个元素中所有元素之和
…,从第二个数集开始,每一个数集比前一个数集多一个元素,且每一个数集中最小的元素比前一个数集中的最大的元素大1,则第n个元素中所有元素之和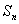 =?
=?
考点说明:等差数列求和
问题解答:本题考查集合和等差数列的综合应用,不妨把题目中的条件简化表示,设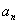 表示第n个数集中元素的个数,那么根据题意,
表示第n个数集中元素的个数,那么根据题意,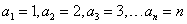 ,也就是
,也就是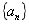 是首项为1,公差为1的等差数列,根据等差数列求和公式,前
是首项为1,公差为1的等差数列,根据等差数列求和公式,前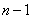 项的和为
项的和为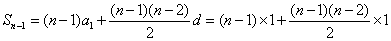 ,化简可以得到
,化简可以得到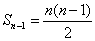 。(注:也可以通过先求
。(注:也可以通过先求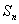 ,在用
,在用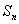 减去
减去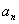 得到
得到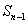 ,这样计算更加方便)
,这样计算更加方便)

微信小程序
微信扫一扫体验

微信公众账号
微信扫一扫加关注
评论 返回
顶部

发表评论 取消回复