高考数学(文科)小题狂做·基础篇
P48 Q9、10、11、12
已知向量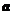 与
与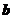 不共线,
不共线,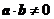 ,且
,且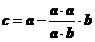 ,则
,则 与
与 的夹角为 ( )
的夹角为 ( )
A.0
B.
C.
D.
考点说明:平面向量数量积的应用(求向量的夹角)
问题解答:由公式知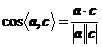 ,而
,而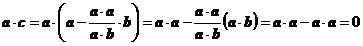 ,从而
,从而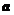 与
与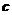 垂直,即所求夹角为90°。
垂直,即所求夹角为90°。
设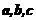 是单位向量,且
是单位向量,且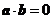 ,则
,则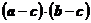 的最小值为 ( )
的最小值为 ( )
A.-2
B.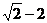
C.-1
D.
考点说明:平面向量的数量积
问题解答: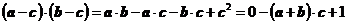 ,要求其最小值,即要求
,要求其最小值,即要求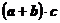 的最大值;而
的最大值;而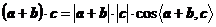 ,显然
,显然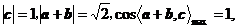 故
故 的最大值为
的最大值为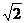 ,从而原式最小值为
,从而原式最小值为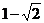 。
。
已知△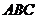 的外接圆圆心为
的外接圆圆心为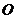 ,半径为2,
,半径为2,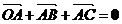 ,且
,且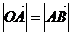 ,则
,则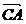 在
在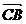 方向上的投影为 ( )
方向上的投影为 ( )
A.-3
B.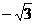
C.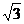
D.3
考点说明:平面向量的数量积的应用(射影的计算)
 问题解答:由
问题解答:由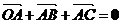 可知
可知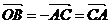 ,从而
,从而 是平行四边形;又由
是平行四边形;又由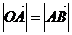 知
知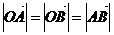 ,从而
,从而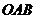 是等边三角形;故
是等边三角形;故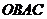 是边长为2的菱形,画出示意图,易知
是边长为2的菱形,画出示意图,易知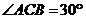 ,从而所求射影长为
,从而所求射影长为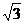 。
。
如图(图略),在Rt△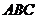 中,
中,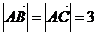 ,且
,且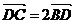 ,点
,点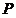 是线段
是线段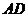 上任一点,则
上任一点,则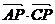 的取值范围是 ( )
的取值范围是 ( )
A.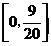
B.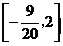
C.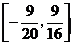
D.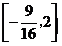
考点说明:平面向量的数量积
问题解答:本题的背景在等腰直角三角形中,建系用坐标进行运算较为简便;注意不要受原图干扰,将图旋转成方便建系的样子
以点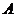 为坐标原点,
为坐标原点,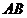 为
为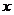 轴,
轴,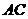 为
为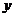 轴建立平面直角坐标系,则
轴建立平面直角坐标系,则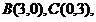 由
由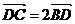 易知
易知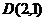 ;设
;设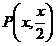 ,便可将
,便可将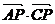 转化为一个关于
转化为一个关于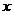 的二次式,考虑
的二次式,考虑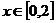 根据二次函数的值域便可求得所求取值范围。
根据二次函数的值域便可求得所求取值范围。

微信小程序
微信扫一扫体验

微信公众账号
微信扫一扫加关注
评论 返回
顶部

发表评论 取消回复